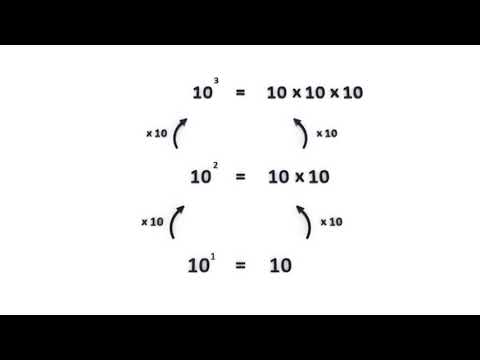Les fractions ont toujours représenté un défi pour les élèves et même pour les enseignants.

Une question se pose alors :

Comment favoriser la construction du concept de la fraction?

Dans l'ensemble des entiers positifs et négatifs, les résultats des opérations d'addition, de soustraction et de multiplication portant sur ces nombres sont des nombres entiers.

Effectivement, lorsque l'on additionne, soustrait et même multiplie deux nombres entiers, le résultat demeure un entier.

Que se passe-t-il lorsque l'on effectue une division d'entiers?

La division des entiers positifs et négatifs n'aboutit pas toujours à un résultat entier.

D'où la nécessité de définir un nouvel ensemble de nombres, les rationnels, dans lequel se trouve le résultat de la division d'entiers. Par exemple, la solution de l'équation : 3 x ? = 2. Cette solution 2/3 est un nombre rationnel que l'on écrira sous la forme d'une fraction d'entiers.


Intuitivement l'enfant a des connaissances liées à la notion des fractions. Il utilise le terme moitié et progressivement, la demie, le tiers et le quart. Comme enseignant, nous réalisons que l'apprentissage du vocabulaire est un apprentissage en soit. Il est important de ne pas prendre pour acquis la compréhension du vocabulaire associé au concept de la fraction. Par exemple, deux tiers peut n'avoir aucun sens pour un enfant!

Ces éléments doivent être utilisés pour construire le concept de fraction.

Or, la construction du concept passe par les sens attachés au concept de fraction.

Des modèles sont utilisés pour y parvenir.

Dans cette capsule, nous regardons plus attentivement les modèles suivants :

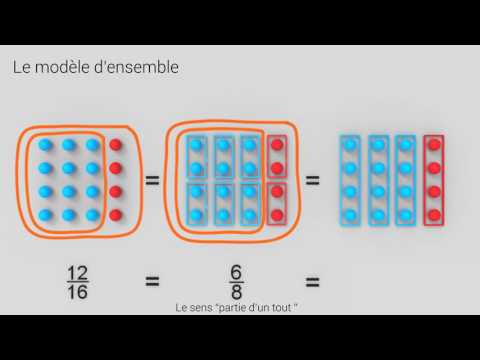
• Le modèle d'ensemble;
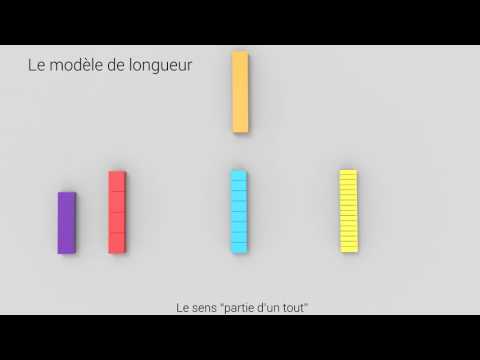
• Le modèle de longueur;
• Le modèle de surface;

Nous notons l'importance des modèles pour éviter la confusion d'une fraction exprimée uniquement de manière symbolique.

Avec la participation de :

Adolphe Adihou, Ph.D.
Anne-Julie Leroux
Olivier Brisson

Une fraction est le représentant d'une famille de fractions.

Qu'est-ce que cela signifie ?

Une fois le sens de la fraction abordé à l'aide de différents modèles tels le modèle d'ensemble, le modèle de longueur ou le modèle de surface, nous comprenons que la fraction ne donne aucune indication quant à la grandeur du tout ou des parties. Il est possible de comparer deux fractions à l'aide d'un modèle que si elles font partie d'un même tout.

Une fraction indique simplement la relation entre la partie et le tout.

Les modèles conceptuels permettront aux élèves de comprendre que deux fractions sont équivalentes si elles constituent deux représentations d'une même quantité. Nous favorisons ici la création d'image mentale à travers une méthode intuitive.

« ATTENTION! Pour développer le concept de « fractions équivalentes », il ne suffit pas de travailler la production de fractions équivalentes ».

Des modèles sont utilisés :

• Le modèle de surface
• Le modèle de longueur
• Le modèle d'ensemble

Comment générer des fractions équivalentes?


Par amplification



Puisque multiplier par 1 ne change pas la valeur de la fraction et que 1 est l'élément neutre de la multiplication.

OU


Par simplification



Puisque diviser par 1 ne change pas la valeur de la fraction.

Avec la participation de :

Adolphe Adihou, Ph.D.
Anne-Julie Leroux
Olivier Brisson

Il existe plusieurs façons de comparer des fractions, inutile de penser que de mettre les fractions sur le même dénominateur est nécessaire. Il suffit d'avoir une bonne compréhension de la fraction.

Tout d'abord, nous comparons des fractions ayant le même dénominateur à l'aide d'un même tout.

À l'aide du modèle de surface, illustrons avec deux feuilles de papier équivalentes représentant un même tout et subdivisées en 5 parties égales, comment comparer 3/5 et 2/5. En superposant les feuilles de papier subdivisées, on déduit que 3/5 est supérieur à 2/5.

Regardons maintenant la comparaison de deux fractions ayant le même dénominateur en utilisant le modèle de longueur.
Fractionnons notre entier de départ en cinq parties égales.
Le bâtonnet bleu représente 3 parties sur 5 parties en tout.
Le bâtonnet rouge représente 2 parties sur 5 parties en tout.
Donc, 3/5 est supérieur à 2/5.

Regardons maintenant lorsque les deux fractions sont unitaires. Il n'est pas nécessaire de les mettre sur un même dénominateur, voici comment il est possible de les comparer.
Représentons chacune des fractions à l'aide d'un même tout.
Regardons les deux animations suivantes.

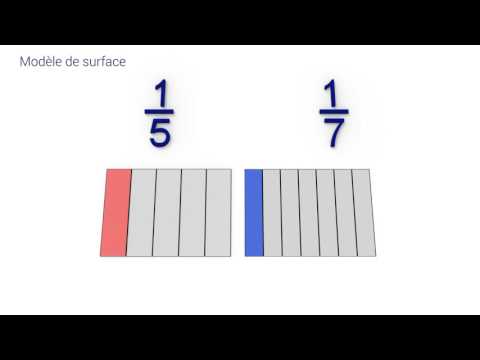
Pour comprendre la comparaison de fractions unitaires en utilisant le modèle de surface.
Superposons nos deux feuilles de papier équivalentes subdivisées respectivement en 5 et 7 parties égales.
Nous constatons que 1/5 est supérieur à 1/7.

Illustrons la fraction 1/5 en fractionnant le bâtonnet vert en 5 parties équivalentes et la fraction 1/7 en le fractionnant en 7 parties équivalentes. En comparant une partie de ce qui est fractionné en 5 parties et en ce qui est fractionné en 7 parties, nous constatons que 1/5 est supérieur à 1/7.


Voici une troisième situation possible. Si les deux fractions ont le même numérateur différent de 1, il est possible de les comparer sans les mettre sur le même dénominateur.

Regardons une illustration intéressante à l'aide du modèle de surface.
Une fois les deux fractions illustrées à l'aide de notre entier de départ.
Nous superposons les deux feuilles comme support, pour les comparer.
Ici, on déduit que, 4/5 est supérieur à 4/7!

Illustrons maintenant cette situation à l'aide du modèle de longueur.
Fractionnons notre entier de départ, le bloc turquoise, en 5 parties égales et respectivement en 7 parties égales.
La fraction 4/5 est représentée par le bâtonnet rose qui représente 4 parties sur 5 parties en tout. La fraction 4/7 elle, est représentée par le bâtonnet bleu qui représente 4 parties sur 7 parties en tout.

La comparaison à l'aide du modèle de longueur, comme support, nous permet d'observer que 4/5 est supérieur à 4/7.


Voici une quatrième situation.
Si les deux fractions ont deux dénominateurs quelconques, il faut regarder le plus petit commun multiple.
Par exemple,


Comparons deux fractions 5/8 et 7/12. Remarquons que les dénominateurs ont un diviseur commun 4.
Fractionnons notre entier de départ en 8 parties égales et respectivement en 12 parties égales.
Le bâtonnet bleu représente 7 parties sur 12 parties en tout et le bâtonnet jaune représente 5 parties sur 8 parties en tout.
En superposant le bâtonnet jaune et bleu, on déduit que 5/8 est supérieur à 7/12.
Toutefois, nous pouvons fractionner l'entier de départ en 24 parties, ce qui est le plus petit multiple commun. Le bâtonnet jaune représente ici 15 parties sur 24 parties en tout, le bâtonnet bleu représente 14 parties sur 24 parties en tout. Alors 5/8 est supérieur à 7/12 puisque 15/24 est supérieur à 14/24.




Comparons deux fractions 5/8 et 7/12 à l'aide du modèle de surface, en faisant du pliage.
Plions les feuilles de papier de deux façons différentes.
Regardons l'animation suivante!
Le premier est fractionné en 24 parties égales et le deuxième aussi en 24 parties égales mais de manière différente.

Toutefois, bien que les parties unitaires n'aient pas les mêmes dimensions, elles ont les mêmes aires.
5/8 est représenté par 15 parties unitaires bleues du premier pliage et 7/12 est représenté par 14 parties unitaires roses du deuxième pliage
Donc 5/8 est supérieur à 7/12 puisque 15/24 est supérieur à 14/24.

En conclusion, l'utilisation d'un modèle joue un rôle important pour la compréhension des élèves. En permettant d'utiliser leurs propres arguments, justifications et méthodes, l'enseignant peut proposer à l'élève de comparer deux fractions qui l'amèneront à explorer les différents modèles. De là l'importance d'insister sur le raisonnement lors des premiers apprentissages des élèves et les soutenir pour les amener progressivement au symbolisme.

Avec la participation de :

Adolphe Adihou, Ph.D.
Anne-Julie Leroux
Olivier Brisson

Pour additionner et soustraire des fractions, évitons l'étude hâtive des règles et algorithmes de calcul sur les fractions.

Voyons plutôt l'addition et la soustraction de fractions comme un jeu d'équivalences.

Une solide compréhension du concept des fractions constitue une base importante pour effectuer des opérations arithmétiques sur les fractions. Dans l'apprentissage des opérations des fractions l'apprenant sera amené d'une manière ou d'autre à utiliser certains sens des fractions, mais aussi le sens des opérations.

A ce propos, il est conseillé d'accompagner les élèves à découvrir et à construire la compréhension autour des opérations sur les fractions que de leur donner les algorithmes.

Soyons conscient de la généralisation que font les élèves à partir des nombres entiers.

L'addition est interprétée comme étant la réunion d'éléments discrets. Alors que la soustraction est la recherche du complément d'un état dont on connaît le total.

Dans les illustrations suivantes, l'unité de référence est différente pour montrer la variabilité.

Il est inutile de penser que de mettre les fractions sur le même dénominateur avant d'effectuer les opérations d'addition et de soustraction est nécessaire lors des premiers apprentissages. Dans certains cas oui, mais dans d'autres non. Il suffit d'avoir une bonne compréhension de la fraction, de l'addition et de la soustraction et utiliser un matériel adéquat et pertinent.

Pour bien comprendre,

Regardons les animations!

Les animations suivantes montrent l'importance de comprendre ce qu'est le tout.

Dans un premier temps, additionnons un entier et une fraction!

À l'aide du modèle de surface, illustrons un (1) par un trapèze rouge qui est l'unité de référence. Ce tout peut être subdivisé en 3 parties égales en d'autres termes par 3 triangles verts. Chaque triangle représente 1/3 par rapport à l'unité de référence. Le losange bleu représente 2 triangles verts, donc 2 triangles verts parmi les 3 qui structurent le tout de référence. En utilisant le sens de l'addition la composition de deux états en un troisième état, on pourra réunir les 3 triangles qui représentent l'entier de référence et les 2 triangles qui représentent 2/3. Nous avons 5 triangles dont chacun représente 1/3.

Regardons maintenant une illustration de la soustraction d'un entier par une fraction.

À l'aide du modèle de surface, illustrons avec 1 par un trapèze rouge qui est l'unité de référence. Ce tout peut être subdivisé en 3 parties égales en d'autres termes par 3 triangles verts. Chaque triangle représente 1/3 par rapport à l'unité de référence. Comment trouver la différence de 1 - 2/3, c'est-à-dire le résultat de la soustraction 1 - 2/3. En utilisant le sens de la soustraction en interprétant l'opération comme la recherche du complément de 2 /3 (illustré par 2 triangles verts) pour avoir 1 (illustré par 3 triangles verts) ou en interprétant la soustraction comme le reste de l'entier 1 lorsque l'on enlève 2/3. Dans tous les cas on a 1 triangle vert soit 1/3.

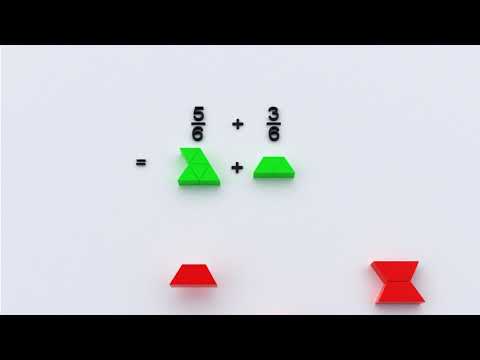
Illustrons l'addition de deux fractions ayant le même dénominateur.

À l'aide du modèle de surface, illustrons par 2 trapèzes rouges accolés, comme l'indique la forme, l'unité de référence. Ce tout peut être subdivisé en 6 parties égales en d'autres termes par 6 triangles verts. Chaque triangle représente 1/6 par rapport à l'unité de référence. 5/6 représente 5 triangles verts parmi les 6 qui structurent le tout de référence et 3/6 représentent 3 triangles verts parmi les 6 qui structurent le tout de référence. Comment trouver la somme de 5/6 et 3/6, c'est-à-dire le résultat de l'addition 5/6 + 3/6. En utilisant le sens de l'addition, nous avons 8 triangles verts dont chacun représente 1/6. La reconfiguration des 8 triangles verts fait ressortir 2 trapèzes rouges accolés, soit l'unité de référence et deux triangles verts. Donc, 5/6 + 3/6 = 1 + 2/6 = 1²⁄₆

Illustrons maintenant la soustraction de deux factions ayant le même dénominateur.

À l'aide du modèle de surface, illustrons par 2 trapèzes rouges accolés, comme l'indique la forme, l'unité de référence. Ce tout peut être subdivisé en 6 parties égales en d'autres termes par 6 triangles verts. Chaque triangle représente 1/6 par rapport à l'unité de référence. 5/6 représente 5 triangles verts parmi les 6 qui structurent le tout de référence et

3/6 représentent 3 triangles verts parmi les 6 qui structurent le tout de référence. Comment trouver la différence de 5/6 - 3/6, c'est-à-dire le résultat de la soustraction 5/6 - 3/6? En utilisant le sens de la soustraction en interprétant l'opération comme la recherche du complément de 3/6 (illustré par 3 triangles verts) pour avoir 5/6 (illustré par 5 triangles verts) ou en interprétant la soustraction comme le reste de 5/6 lorsque l'on enlève 3/6. Dans tous les cas on a 2 triangles verts soit 2 fois 1/6 = 2/6.

Notons que cette illustration met en évidence le sens de partie d'un tout d'une fraction, mais aussi le sens des opérations. Pour un premier apprentissage, l'apprenant découvre comment générer la somme et la différence de fractions, mais par contre la fraction est perçue comme une fraction quantité. Il serait utile d'utiliser d'autres sens qui mettent en évidence la fraction relation.

Nous venons de montrer une approche qui permet de développer du sens autour de l'addition et de la soustraction de fractions. Maintenant, utilisons le concept des fractions équivalentes pour additionner et soustraire des fractions.

Si nous voulons additionner ou soustraire 5/8 et 7/12, nous pouvons transformer 5/8 en une fraction équivalente 15/24 et 7/12 en 14/24.

L'algorithme vient à la rescousse, si le jeune s'est impliqué dans sa construction et qu'il lui a donné du sens.

Les illustrations nous montrent bien la variété d'écriture possible pour une même fraction. Or, aucune convention oblige à simplifier le résultat!

Avec la participation de :

Adolphe Adihou, Ph.D.
Anne-Julie Leroux
Olivier Brisson

Avec la participation de :

Adolphe Adihou, Ph.D.
Anne-Julie Leroux
Olivier Brisson

Il est inutile de penser que tous les nombres écrits avec une virgule sont des nombres décimaux.

Les nombres entiers sont des nombres décimaux mais nous n'utilisons pas de virgule pour les écrire.

Par exemple, 17 est un nombre décimal.

D'un autre côté, nous utilisons une virgule pour écrire des nombres, mais ce ne sont pas des nombres décimaux.

1,333333333….= ⁴⁄₃, n'est pas un nombre décimal et il en est de même pour π.

Il est nécessaire lors des premiers apprentissages de distinguer la définition d'un objet mathématique (ce qu'est un nombre décimal) et sa représentation (comment représenter cet objet). Dans certains cas, il est difficile de dissocier ces deux aspects.

Qu'est-ce qu'un nombre décimal?

Un nombre décimal est un nombre rationnel (particulier). Si un nombre rationnel est tout nombre qui peut s'écrire sous la forme ^a⁄_b avec a un nombre entier et b un nombre entier non-nul, tout nombre rationnel ^a⁄_b qui possède des fractions équivalentes dont le dénominateur est une puissance de 10 (10, 100, 1000,…) est un nombre décimal.

Cette définition s'appuie sur l'ensemble d'appartenance du nombre et sa représentation

On peut représenter un nombre décimal sous forme fractionnaire, c'est le cas des fractions décimales (Exemple : ⁵³⁄₁₀₀ )

On peut aussi représenter un nombre décimal en utilisant un développement décimal (exemple : 0,53).

À ce propos : ⁵³⁄₁₀₀ = 0,53. Nous avons ici une fraction de la forme ^a⁄_b avec a un nombre entier et b un nombre entier non-nul.

et 1,333333333…..= ⁴⁄₃ , est-il un nombre décimal?

Une question se pose alors!

Existe-t-il une fraction équivalente dont le dénominateur est une puissance de 10?

Or, ⁴⁄₃ n'est pas un nombre décimal car on ne peut pas trouver une fraction équivalente à ⁴⁄₃ dont le dénominateur est une puissance de 10.

Ce n'est pas que la virgule qui donne le statut d'un nombre décimal!

Lorsqu'un nombre décimal s'écrit sous la forme d'un développement décimal, il comporte deux parties (une partie entière et une partie fractionnaire) séparées par une virgule (du point de vue représentation) qui respecte les propriétés de la numération de position décimale.

Par exemple: 17,94

Nous avons la partie entière : 17 et la partie fractionnaire : ⁹⁴⁄₁₀₀

Une solide compréhension du concept des nombres décimaux constitue une base importante pour distinguer les nombres, effectuer des opérations arithmétiques et d'autres activités en mathématiques qui font appel aux nombres.

Dans l'apprentissage des nombres décimaux l'apprenant sera amené d'une manière ou d'une autre à utiliser et à distinguer les nombres. Il est conseillé d'accompagner les élèves pour découvrir et à construire la compréhension autour des nombres décimaux en les faisant verbaliser. Il existe plusieurs activités pour construire le sens autour des nombres décimaux : la lecture, l'écriture et la décomposition des nombres décimaux.

Il est possible d'introduire les nombres décimaux avec différents matériels. Par exemple, les blocs multibases, les outils de mesure (longueur, masse, volume), la monnaie et la droite numérique.

Il est important de demeurer conscient des limites de chaque matériel.

Voyons des exemples!

Prenons le cas des Blocs multibases :

Tout comme dans l'apprentissage des fractions, le recours à l'unité de référence est important.

Le gros cube est l'unité de référence. Si le gros cube est l'unité de référence, alors la plaquette est le dixième du gros cube. Le bâtonnet est le dixième de la plaquette, donc le centième du gros cube. Et finalement, le petit cube est le dixième du bâtonnet, donc le centième de la plaquette et le millième du gros cube.

Selon cette unité de référence, représentons 1, 234 à l'aide des blocs multibases;

Une unité représentée par un gros cube, deux plaquettes représentant deux dixièmes, trois bâtonnets représentant trois centièmes et finalement quatre petits cubes représentant quatre millièmes.

Donc,

1,234=¹²³⁴⁄₁₀₀₀=1234 _x10^-3

Une fois les nombres représentés, on peut opérer sur ceux-ci.

Regardons une deuxième illustration 3D

Si l'unité de référence est la plaquette, le gros cube représente une dizaine c'est-à-dire dix unités, le bâtonnet représente un dixième de la plaquette et le petit cube le centième de la plaquette.

Selon cette unité de référence, représentons 5, 67 (cinq virgule 67) à l'aide des blocs multibases.

Nous avons 5 plaquettes représentants 5 unités, 6 bâtonnets représentants six dixièmes et 7 petits blocs représentants sept centièmes.

Dans ce cas, nous pouvons représenter le nombre

5,67=⁵⁶⁷⁄₁₀₀=567 _x10^-2

Remarquons que tout matériel de manipulation à des limites. Il en est de même pour les blocs multibases. En effet, vu l'exemple précédant, si la plaquette représente l'unité de référence, les blocs multibases ne fournissent pas une représentation des millièmes. Cette limite oblige à passer à une autre forme de représentation et de symbolisation.

Ces subdivisions reviennent à mettre en évidence les positions de numération décimale et à y donner sens.

Utilisons maintenant la droite numérique

Représentons quelques nombres décimaux entre 5 et 6 en utilisant la droite numérique.

Est-il possible de tous les représenter?

Illustrons 5 et 6 à une certaine distance sur un segment de droite. Ensuite, subdivisons cet espace en dix parties égales.

Chaque partie représente la dixième partie de l'espace initial. En subdivisant cet espace en 100 parties égales, nous obtiendrons la centième partie de l'espace, etc…

Avec la participation de :

Adolphe Adihou, Ph.D.
Anne-Julie Leroux
Olivier Brisson

En enseignement et en apprentissage des mathématiques, nous sommes appelés à déterminer les mesures de certains objets géométriques en 0, 1, 2 ou 3 dimensions.
Il s'agit du point, du segment de droite, de la figure plane en dimension deux ou du solide.

Le point est de dimension 0.
La longueur est vue en dimension 1.
L'aire en dimension 2.
Le volume en dimension 3.

Par ailleurs, comme tout concept mathématique, la mesure se développe à travers des stades et des étapes d'apprentissage comme l'ont mis en évidence plusieurs chercheurs.

Quatre étapes sont nécessaires à tout apprentissage de la mesure :

1. Une approche de la notion de mesure indépendamment de la mesure;
2. La nécessité de mesurer et les premières mesures naturelles;
3. La découverte des unités conventionnelles de mesure;
4. Les formules et les instruments de mesure.

L'enseignement et l'apprentissage de la mesure des objets géométriques reposent sur des processus. Un défi se pose à l'enseignant et à l'élève.
Comment trouver la mesure de certains objets géométriques?

Il est important d'aborder la construction de la mesure en recourant d'abord aux objets physiques. Ce recours impose une démarche de mesure qui consiste à associer un nombre à une grandeur par recouvrement de l'espace à mesurer.

On pourrait commencer par les types d'espace à mesurer : la longueur (dimension 1), ensuite l'aire (dimension 2) et le volume (dimension 3).

Comme tout concept mathématique, L'apprentissage de la mesure ne se fait pas sans obstacle.


Lors des premiers apprentissages, il est conseillé d'utiliser des unités de mesures non conventionnelles comme plusieurs recherches l'ont démontré.

Par exemple, quelle est la longueur de la chaise du sol au sommet du dossier en utilisant le crayon comme unité de mesure.

Relativement à cette unité de mesure, l'espace à mesurer est de 1, 2, 3, 4, 5 unités complètes et la moitié de l'unité.
Le processus peut être aussi appliqué pour déterminer l'aire d'une surface en utilisant le carré-unité ou le volume d'un solide en utilisant le cube-unité.

L'utilisation d'unités non conventionnelles dans le cadre des objets géométriques invite l'apprenant à se concentrer plus directement sur l'attribut à mesurer et lui fournit de bonnes raisons d'employer des unités conventionnelles.

Notons que l'estimation d'une mesure est un processus à ne pas négliger dans l'enseignement du concept. Elle permet de mesurer ou d'établir des comparaisons à partir d'informations visuelles ou mentales, sans utiliser d'instrument particulier.

Il en est de même pour les mesures qualitatives ce qui permet d'établir ou non des relations directes entre les types de mesure - c'est le cas de l'aire et du périmètre par exemple - ou de travailler les conflits qui peuvent exister entre l'aire et le périmètre de figure lorsque vient le moment de travailler ces aspects.

Regardons maintenant l'apprentissage des formules!




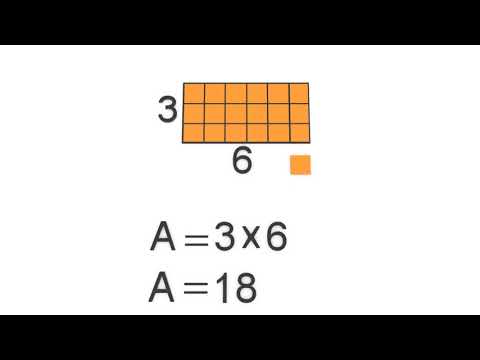
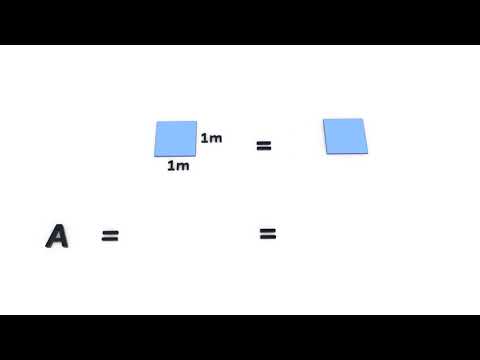
Recouvrons le rectangle de départ par les carré-unités. Alors, l'aire de ce rectangle est de 18 carré-unités. Réciproquement, les côtés du rectangle de départ mesurent 6 unités par 3 unités de longueur. On retrouve l'aire de 18 carré-unités du rectangle en multipliant les deux mesures de côté.

Par cette illustration, une généralisation montre que l'aire d'un rectangle est égale à la mesure de sa longueur multipliée par la mesure de sa largeur.


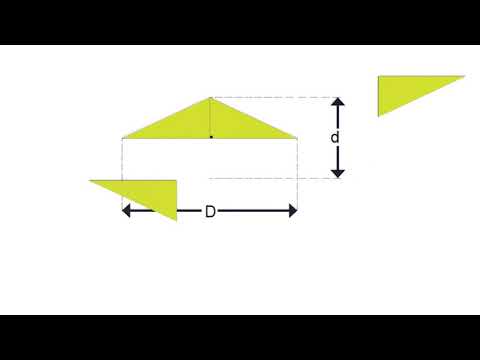
Comment établir l'aire du parallélogramme en connaissant le processus qui permet d'établir l'aire du rectangle? Deux des multiples caractéristiques du parallélogramme sont sa base et sa hauteur. Regardons l'animation!
À partir du parallélogramme dont la base mesure 5 unités et la hauteur 3 unités, nous générons un rectangle de même aire ayant la même mesure de base et la même hauteur.
Par le même processus que pour l'aire du rectangle, nous remarquons que l'aire est égale au produit de la mesure de la base et de la hauteur.


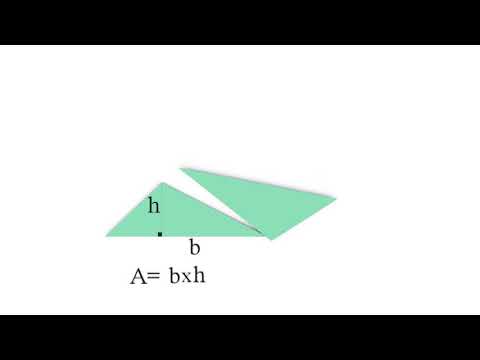
Illustrons une fa¸on de déterminer l'aire du triangle à partir du parallélogramme.
Formons un parallélogramme à partir du triangle par des transformations montrées par l'illustration. L'aire du parallélogramme est bien la mesure de la base multipliée par la mesure de la hauteur. Puisque l'aire du parallélogramme est le double de l'aire du triangle de départ, l'aire du triangle est égale à la mesure de la base multipliée par la mesure de la hauteur divisée par 2.




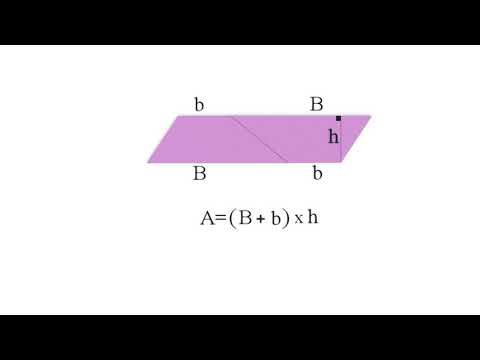
Par le même processus que dans le cas du triangle, les transformations permettent d'obtenir un parallélogramme dont la base est la somme de la mesure des bases du trapèze de départ et de même mesure de hauteur. L'illustration met en évidence la formule de l'aire du trapèze.

Considérons un losange en identifiant les mesures des deux diagonales. À l'aide de transformations géométriques, nous formons un rectangle dont la mesure de la base correspond à la mesure de la grande diagonale et la mesure de la hauteur correspond à la moitié de la petite diagonale. L'aire est obtenue en multipliant ces deux mesures.


Remarquons qu'il existe d'autres transformations géométriques qui permettent d'établir les formules. À ce propos, il faut offrir des occasions diversifiées à nos élèves pour les expérimenter.

Avec la participation de :

Adolphe Adihou, Ph.D.
Anne-Julie Leroux
Olivier Brisson

Dans l'enseignement et l'apprentissage des mathématiques ainsi que dans la vie active, nous sommes régulièrement amenés à effectuer des transformations d'unités de mesure.

Voici des approches didactiques intéressantes permettant de donner du sens aux diverses transformations d'unités de mesures de longueur, de masse et de capacité.

L'unité de référence pour les longueurs est le mètre. Pour la masse, il s'agit du gramme et pour la capacité, le litre est l'unité de référence.

Regardons l'animation suivante!


Pourquoi 3 mètres = 30 décimètres

Et maintenant,

Pourquoi 5 hectomètres = 5000 décimètres


Quand on s'intéresse aux relations multiplicatives dans les transformations des mesures, le lien se fait entre les multiples et les sous-multiples de l'unité avec des facteurs qui pourraient être des puissances de 10.

L'animation suivante permet par observation et déduction d'expliquer le passage d'une puissance à une autre. Des préfixes font le lien entre les multiples et les sous-multiples, issus des subdivisions de 10. Nous débutons l'animation par 10 exposant 1 égal à 10. Par le biais de propriétés mathématiques, nous retrouvons la valeur des puissances supérieures à 1 et des puissances inférieures à 1 entre autres, 10 exposant 0 égal 1.



Le tableau suivant illustre les facteurs puissances de 10 et les préfixes. Par exemple, le préfixe déci- est la dixième partie de l'unité et le préfixe déca- est dix fois l'unité.

Quelles sont les influences de ces transformations d'unités sur l'aire et le volume ?



Regardons l'animation suivante !



Les relations mathématiques sont transférables et montrent en détail les équivalences qui permettent les transformations d'unités d'aire et de volume. En tant qu'enseignant, une attention particulière doit être portée à la construction de sens dans les transformations de mesures ainsi qu'au sens des préfixes et à leurs valeurs numériques lors des conversions et la construction des tableaux de conversions

Avec la participation de :

Adolphe Adihou, Ph.D.
Anne-Julie Leroux
Olivier Brisson